子集构造法的一个 Haskell 实现,我不喜欢长篇大论的贴代码,把自动机这一部分放到了 Gist,项目地址: higuoxing/hregex
Update: 2018.03.05
用字符来描述状态的改变其实效率是很低的,试想一下UTF-8的字符集有多大?如果只使用字符来描述状态的改变生成的DFA是很大的,所以可以利用字符集来描述状态的改变,当利用这样的边时,在匹配字符上就可以利用BST了,并且在建立DFA时也省事许多,拥有更高的效率,可以这样做
data Transition state = Edge state (Set Char) state
| Epsilon (Int, Int) state
可以参考这个答案 Stack Overflow
Introduction
本文主要是对编译原理[1]中比较经典的「不确定有穷自动机」Nondeterministic Finite Automata转为「确定的有穷自动机」Deterministic Finite Automata算法的一个实践,寒假时看了些有关函数式编程的东西,所以这里就拿Haskell来当做工具了,这里就先不对效率有什么要求,主要阐述自动机的构造方法和转换。
Automata Structure
自动机在很多情况下是被定义成一个5元-元组tuple
$$FA = <Q, \Sigma, \delta, q_0, F>$$
其中
Q : 自动机中所有的状态集合
Sigma : 自动机中所有的标志(symbols)集合
delta : 自动机中所有的状态转换集合 (map (Q, Sigma)-> Q)
q_0 : 自动机的初始状态
F : 自动机所有终结状态的集合
所以根据定义,我们可以得到一个有限自动机(FA)的构造函数
Automata
data Automata state where
Automata :: (Ord state, Show state)
=> Set state -- Finite set of states
-> Set Char -- Set of input char
-> Set (Transition state) -- Transition functions (s1 -(char|epsilon)-> s2)
-> state -- Initial state
-> Set state -- Set of acceptable states
-> Automata state
data Transition state = Edge state Char state
| Epsilon state state
deriving (Ord, Eq, Show)
Algorithm
子集构造法的伪码如下,十分短小
Pseudo code for subset construction
Initially, epsilon-closure(s0) only state in Dstate, unmarked
while unmarked state T in Dstate do
mark T;
for each input symbol a do
U := epsilon-closure(move(T, a))
if U is not in Dstates then
add U as an unmarked state to Dstates
Dtran[T, a] := U
end
end
其中, epsilon-closure(s) 是所有NFA的状态中可以并且只通过epsilon边转换能够到达的NFA状态集合,epsilon-closure(T) 是能够从状态集合T中任意一个状态开始只通过epsilon边转化到达的NFA状态集合,move(T, a) 是能够从状态集合T中通过标记为a的边转换到达的NFA状态集合
以上三个闭包的求法大致相同,epsilon-closure(s)可以看做是epsilon-closure(T)的一个特殊情况,其中T只含有s一个元素,而求epsilon闭包只需要一个简单的深度优先遍历(DFS)算法即可
epsilonClosure_T
-- set of states that transfered from state s via epsilon edge
epsilonClosure_T :: Ord state => Automata state -> Set state -> Set state
epsilonClosure_T (Automata ss_ cs ts s_ terms) ss = epsilonClosure_T'
(Set.filter isEpsilon ts)
(Set.toList ss) ss
epsilonClosure_T’ 辅助函数
epsilonClosure_T' :: Ord state => Set (Transition state) -> [state] -> Set state -> Set state
epsilonClosure_T' ts [] ss = ss
epsilonClosure_T' ts (st:stack) ss = epsilonClosure_T' ts stack' ss'
where
epm = epsilonMoveFrom ts st
ss' = Set.union ss epm
stack' = stack ++ Set.toList (Set.difference ss' ss)
-- one epsilon move from state s
epsilonMoveFrom :: (Eq state, Ord state) => Set (Transition state) -> state -> Set state
epsilonMoveFrom ts s = Set.foldr f Set.empty ts
where
f t set | t `isEpsilonMoveFrom` s = let (s0, s1) = getStates t in Set.insert s1 set
| otherwise = set
以上,之所以使用了另外一个epsilonClosure_T'这个辅助函数是因为我们需要一个栈来保存一些仍可能发出epsilon边的状态,这样通过下一次调用就可以得到通过这些状态经epsilon边到达的另外一部分状态,move(T, a)的算法与求epsilon闭包的算法相近,只不过不需要深度优先遍历而已
move_T
-- move(T, c, s) :: Ord state => Automata state -> Set state -> Char -> Set state
-- set of states that transifered from state s via Char c
move_T :: Ord state => Automata state -> Set state -> Char -> Set state
move_T (Automata ss_ cs ts s_ terms) ss c = Set.foldr f Set.empty ss
where
f x set = Set.union set (transitionFrom ts x c)
-- one transition from state s via c
transitionFrom :: (Eq state, Ord state) => Set (Transition state) -> state -> Char -> Set state
transitionFrom ts s c = Set.foldr f Set.empty ts
where
f t set | isTransitionMoveFrom t s c = let (s0, s1) = getStates t in Set.insert s1 set
| otherwise = set
剩下的便是将它们组合成子集构造法的函数,根据以往的经验,伪码中又出现了循环,所以利用递归解决掉它,首先根据我们的需求来确定它的函数签名,接受一个NFA返回一个DFA
subsetConstruct
-- transform NFA to DFA using subset construction
subsetConstruct
:: (Ord state, Eq state) => Automata state
-> Automata (Set state)
subsetConstruct nfa@(Automata ss cs ts s_ terms)
= subsetConstruct' nfa iniDFA iniUdss
where
iniDFA = Automata (Set.empty) cs (Set.empty) (s_ini) (Set.empty)
s_ini = epsilonClosure_T nfa (Set.fromList [s_])
iniUdss = Set.fromList [s_ini]
之后,就只需要构造这个递归的subsetConstruct'的辅助函数了,根据上面我们求epsilon闭包的辅助函数,我们还是把unmarked Dstates放到一个叫做udss的栈来时时保存还没有标记的状态,也就是说,我们的辅助函数只要接受一个NFA,一个时时改变的DFA和一个保存着未标记状态的栈即可,当栈为空时返回DFA即可
Tips: 这里有个小坑是在udss保存未标记的状态时,注意不要把空状态误加入,否则会出现一个空状态,影响后面程序
subSetconstruct’ 辅助函数
subsetConstruct'
:: (Ord state, Eq state) => Automata state
-> Automata (Set state) -> Set (Set state) -> Automata (Set state)
subsetConstruct' nfa@(Automata ss cs ts s_ terms) dfa@(Automata dss dcs dts ds_ dterms) udss
| Set.null udss = dfa
| otherwise = subsetConstruct' nfa (Automata dss' dcs' dts' ds_ dterms') udss'
where
(tset, udss'') = popDstate udss -- pop T from unmarked Dstates
dss' = addDstate tset dss -- mark dstate
dcs' = dcs -- just copy dcs
(udss', dts') = addTrans nfa (Set.toList dcs) tset dss' dts udss''
dterms' = if isTerm tset terms then -- add dterms
addDstate tset dterms
else dterms
然后根据我们的需要去把自动机声明为Show的实例(instance)即可加载到解释器验证了,这里拿一个栗子(a|b)*aa进行验证…
上面正则表达式构成的NFA为:
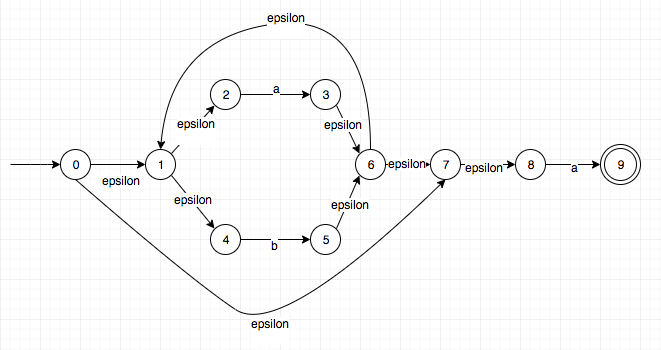
转换后的DFA为:
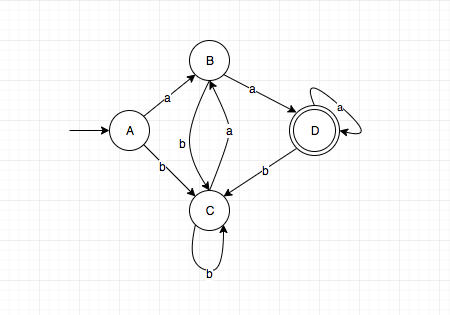
A = {0, 1, 2, 4, 7}
B = {1, 2, 3, 4, 6, 7, 8}
C = {1, 2, 4, 5, 6, 7}
D = {1, 2, 3, 4, 6, 7, 8, 9}
可验证
$ ghci
GHCi, version 8.2.2: http://www.haskell.org/ghc/ :? for help
Prelude> :l Automata.hs
[1 of 1] Compiling Regex.Automata ( Automata.hs, interpreted )
Ok, one module loaded.
*Regex.Automata> let nfa = Automata (Set.fromList [0..9])
(Set.fromList ['a', 'b'])
(Set.fromList [
Epsilon 0 1 ,
Epsilon 0 7 ,
Epsilon 1 2 ,
Epsilon 1 4 ,
Epsilon 6 1 ,
Edge 2 'a' 3 ,
Edge 4 'b' 5 ,
Epsilon 3 6 ,
Epsilon 5 6 ,
Epsilon 6 7 ,
Edge 7 'a' 8 ,
Edge 8 'a' 9])
0
(Set.fromList [9])
*Regex.Automata> let dfa = subsetConstruct nfa
*Regex.Automata> dfa
states: fromList [
fromList [0,1,2,4,7] , -- A
fromList [1,2,3,4,6,7,8] , -- B
fromList [1,2,3,4,6,7,8,9] , -- D
fromList [1,2,4,5,6,7] -- C
]
input chars: fromList "ab"
transitions: fromList [
Edge (fromList [0,1,2,4,7]) 'a' (fromList [1,2,3,4,6,7,8]) ,
Edge (fromList [0,1,2,4,7]) 'b' (fromList [1,2,4,5,6,7]) ,
Edge (fromList [1,2,3,4,6,7,8]) 'a' (fromList [1,2,3,4,6,7,8,9]),
Edge (fromList [1,2,3,4,6,7,8]) 'b' (fromList [1,2,4,5,6,7]) ,
Edge (fromList [1,2,3,4,6,7,8,9]) 'a' (fromList [1,2,3,4,6,7,8,9]),
Edge (fromList [1,2,3,4,6,7,8,9]) 'b' (fromList [1,2,4,5,6,7]) ,
Edge (fromList [1,2,4,5,6,7]) 'a' (fromList [1,2,3,4,6,7,8]) ,
Edge (fromList [1,2,4,5,6,7]) 'b' (fromList [1,2,4,5,6,7])
]
initial state: fromList [0,1,2,4,7]
acceptable states fromList [fromList [1,2,3,4,6,7,8,9]]
Conclusion
至此,子集构造法完毕,值得一提的是,自动机还是利用数据结构中的有向图实现效率会比这里用集合更好把握一些,如果将来有时间,我准备利用C++/C来实现以上算法。
Reference
[1] Compilers: Principles, Techniques, and Tools (2nd Edition)
[2] From NFA to DFA